Hook
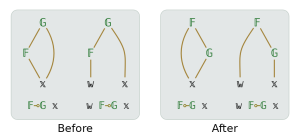
A hook is an asymmetrical form of function composition that first applies one of the composed functions to one argument, then applies the other function to one argument and the result. In J, a 2-train is a hook, while I adds the mirror image to give two functions hook (h) and backhook (H). BQN uses two modifiers Before (⊸) and After (⟜), which also serve the purpose of the Bind operator.
The meaning of 2-train as hook was first proposed in Iverson and McDonnell's paper Phrasal Forms introducing trains[1], and soon included in J. This definition specifies that (F G) y is y F G y and x (F G) y is x F G y. However, Roger Hui later opined that this definition was better suited to a conjunction (dyadic operator) than an element of syntax,[2] and defined to 2-train to represent Atop instead when he led the introduction of trains to Dyalog APL.
In I and BQN, there are two hooks in order to maintain symmetry: for example, BQN defines Before (⊸) to be the 2-modifier {(𝔽𝕨⊣𝕩)𝔾𝕩} ("𝔾's left argument comes from 𝔽") and After (⟜) to be {(𝕨⊣𝕩)𝔽𝔾𝕩} ("𝔽's right argument comes from 𝔾"). In the two-argument case these functions are identical to Reverse Compose and Beside respectively, but in the one-argument case they differ because the argument is used twice: the second function application takes it as an argument directly in addition to the result of the first function application.
Like Reverse Compose, the two hooks can be used together to form a split-compose construct.
3‿¯1‿4 ×⊸×⟜| ¯2‿¯7‿1 ⟨ 2 ¯7 1 ⟩
This definition behaves differently that the Compose-based one when only one argument is given: in that case, it becomes a monadic 3-train.
The name "hook" was chosen based on the hook shape of a function call diagram such as the one below, taken from Phrasal Forms.
⍺(fg)⍵ ←→ ⍺fg⍵
f
/ \
⍺ g
\
⍵
See also
External links
References
- ↑ Ken Iverson and Eugene McDonnell. Phrasal forms at APL89.
- ↑ Roger Hui. Hook Conjunction?. J Wiki essays. 2006. Accessed 2021-02-08.